Bayangkan suatu desa yang terdiri dari 60 keluarga. Misalkan kita ingin mempelajari hubungan antara pengeluaran konsumsi sebagai variabel terikat (Y) dengan pendapatannya sebagai variabel bebas (X). Misalkan 60 keluarga itu dijadikan 10 kelompok berdasarkan kemiripan tingkat pendapata. Data hipotesisnya seperti berikut ini.
Kelompok Pendapatan Keluarga (X) | ||||||||||
80 | 100 | 120 | 140 | 160 | 180 | 200 | 220 | 240 | 260 | |
| Pengeluaran Konsumsi (Y) | 55 | 65 | 79 | 80 93 95 103 108 113 115 | 102 107 110 116 118 125 | 110 115 120 130 135 140 | 120 136 140 144 145 | 135 137 140 152 157 160 162 | 137 145 155 165 175 189 | 150 |
| E(Y|X) | 65 | 77 | 89 | 101 | 113 | 125 | 137 | 149 | 161 | 173 |
sumber: Mulyono, Sri. Statistika Untuk Ekonomi. Edisi kedua. LPFEUI. 2003.
dapat ditafsirkan seperti berikut. Ada 5 keluarga yang pendapatannya 80 dengan tingkat konsumsi antara 55 sampai 75. Dengan kata lain, masing-masing kolom memberikan distribusi pengeluaran konsumsi untuk setiap nilai pendapatan tertentu. Untuk masing-masing distribusi Y dapat dihitung nilai rata-ratanya yang dilambangkan dengan E(Y|X) atau dikenal sebagai conditional mean. Sebagai contoh, E(Y|80) = 1/5(55) + 1/5(60) + 1/5(65) + 1/5(70) + 1/5(75) = 65.
Telah jelas bahwa setiap conditional mean E(Y|Xi) adalah fungsi dari Xi yang dilambangkan E(Y|Xi)=f(Xi). Dalam contoh kita E(Y|Xi) adalah fungsi linier terhadap Xi, misalkan fungsi regresi populasi linier dua variabel itu berbentuk :
E(Y|Xi) = A + BXi
A dan B masing-masing dinamakan intercept dan koefisien kemiringan (slope). Dalam analisis regresi tujuan kita adalah menduga garis regresi populasi atau menduga nilai-nilai A dan B yang tak diketahui berdasar pengamatan variabel-variabel yang terlibat.
Karena titik-titik pasangan (X,Y) tidak semuanya jatuh pada garis regresi populasi, maka hubungan yang pasti seperti ditunjukkan di atas harus dimodifikasi dengan memasukkan unsur kesalahan (random disturbance term, error term, atau stochastic term (u)) sehingga persamaan menjadi :
Yi = A + BXi + u
di mana Yi adalah nilai observasi pengeluaran konsumsi.
Error term (u) dapat timbul melalui beberapa kekuatan yang saling mempengaruhi. Pertama, kesalahan muncul karena model adalah suatu penyederhanaan dari realitas. Kita menganggap bahwa pendapatan merupakan faktor tunggal yang mempengaruhi konsumsi. Kenyataannya, banyak kekuatan yang mempengaruhi tetapi dihilangkan dari analisis misalnya kekayaan, konsumsi tahun lalu, tingkat bunga dan lain-lain dan ini mungkin akan ditangkap dalam error term. Kedua, sumber kesalahan berkaitan dengan pengumpulan dan pengukuran data. Data ekonomi seringkali sulit untuk diukur. Ketiga, karena ksalahan bentuk fungsi yang digunakan. Anda harus ingat bahwa terdapat banyak bentuk fungsi yang menyatakan hubungan antar variabel.
Untuk setiap nilai variabel bebas X, terdapat suatu distribusi probabilitas dari U (error term). Karena itu untuk setiap X terdapat distribusi probabilitas dari Y maupun distribusi probabilitas intercept (a) dan koefisien kemiringan (b).
Sejalan dengan garis regresi populasi, kita dapat menunjukkan garis regresi sampel. Persamaan garis regresi sampel dituliskan sebagai :
^
Yi = a + bXi
dimana :
^
Yi adalah penduga terhadap E(Y|X)
a adalah penduga terhadap A
b adalah penduga terhadap B
Sekarang kita akan menyatakan persamaan garis regresi sampel itu dalam bentuk stochastic seperti berikut :
Yi = a + bXi + ei
dimana ei adalah residual dan ei merupakan penduga terhadap ui.
Akhirnya timbul pertanyaan, bagaimana membentuk persamaan regresi populasi sehingga a sedekat mungkin dengan A (yang sesungguhnya) dan b sedekat mungkin dengan B (yang sesungguhnya)?
Telah disebutkan bahwa dalam analisis regresi tujuan utamanya adalah menduga fungsi regresi populasi berdasar fungsi sampel setepat mungkin. Sampai saat ini ada banyak metode untuk menyusun persamaan regresi sampel, misalnya free hand, least squares dan maximum likelihood. Dalam analisis regresi metode yang paling banyak digunakan adalah metode least squares. Berikut adalah penurunan rumus dari regresi populasi ke metode least squares.
\dpi{120} \epsilon (Y|X)=A+BX_{i} --> model populasi
--> model populasi
 --> model sampel
--> model sampel
 --> bentuk stokastik
--> bentuk stokastik


Dimulai dari rumus di atas, maka dimulailah pencarian metode least squares. Metode least squares merupakan metode yang memiliki jumlah kuadrat kesalahan paling kecil. Artinya meminimumkan :
 atau
atau  atau
atau 
Karena jumlah residual adalah fungsi dari a dan b, dengan proses diferensiasi dihasilkan rumus berikut :
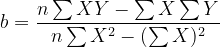 dan
dan 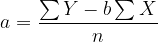
dimana n banyaknya observasi.
Bila persamaan regresi sampel telah dibentuk maka kurva yang sesuai dapat dibuat lebih mudah. Penduga yang diperoleh melalui prinsip least squares dinamakan penduga least squares.
Sementara itu garis regresi sampelnya memiliki ciri-ciri:
Contoh: suatu sampel random sebanyak 10 keluarga bertujuan untuk melihat hubungan antara pengeluaran konsumsi (Y) dengan pendapatan keluarga (Xi). Hasil pengamatan itu dapat dilihat pada tabel di bawah ini.
sumber: Mulyono, Sri. Statistika Untuk Ekonomi. Edisi kedua. LPFEUI. 2003.
Jawab:


sehingga persamaan regresi sampelnya :
ini berarti bahwa jika X naik satu satuan maka Y akan bertambah sebesar 0,5091. Bila b = 0 berarti tak ada hubungan antara Y dan X dan regresi sampelnya merupakan garis horizontal. Garis regresi sampel dapat digambarkan dengan mengambil dua pasang titik (X,Y) secara sembarang.
Telah jelas bahwa setiap conditional mean E(Y|Xi) adalah fungsi dari Xi yang dilambangkan E(Y|Xi)=f(Xi). Dalam contoh kita E(Y|Xi) adalah fungsi linier terhadap Xi, misalkan fungsi regresi populasi linier dua variabel itu berbentuk :
E(Y|Xi) = A + BXi
A dan B masing-masing dinamakan intercept dan koefisien kemiringan (slope). Dalam analisis regresi tujuan kita adalah menduga garis regresi populasi atau menduga nilai-nilai A dan B yang tak diketahui berdasar pengamatan variabel-variabel yang terlibat.
Karena titik-titik pasangan (X,Y) tidak semuanya jatuh pada garis regresi populasi, maka hubungan yang pasti seperti ditunjukkan di atas harus dimodifikasi dengan memasukkan unsur kesalahan (random disturbance term, error term, atau stochastic term (u)) sehingga persamaan menjadi :
Yi = A + BXi + u
di mana Yi adalah nilai observasi pengeluaran konsumsi.
Error term (u) dapat timbul melalui beberapa kekuatan yang saling mempengaruhi. Pertama, kesalahan muncul karena model adalah suatu penyederhanaan dari realitas. Kita menganggap bahwa pendapatan merupakan faktor tunggal yang mempengaruhi konsumsi. Kenyataannya, banyak kekuatan yang mempengaruhi tetapi dihilangkan dari analisis misalnya kekayaan, konsumsi tahun lalu, tingkat bunga dan lain-lain dan ini mungkin akan ditangkap dalam error term. Kedua, sumber kesalahan berkaitan dengan pengumpulan dan pengukuran data. Data ekonomi seringkali sulit untuk diukur. Ketiga, karena ksalahan bentuk fungsi yang digunakan. Anda harus ingat bahwa terdapat banyak bentuk fungsi yang menyatakan hubungan antar variabel.
Untuk setiap nilai variabel bebas X, terdapat suatu distribusi probabilitas dari U (error term). Karena itu untuk setiap X terdapat distribusi probabilitas dari Y maupun distribusi probabilitas intercept (a) dan koefisien kemiringan (b).
Sejalan dengan garis regresi populasi, kita dapat menunjukkan garis regresi sampel. Persamaan garis regresi sampel dituliskan sebagai :
^
Yi = a + bXi
dimana :
^
Yi adalah penduga terhadap E(Y|X)
a adalah penduga terhadap A
b adalah penduga terhadap B
Sekarang kita akan menyatakan persamaan garis regresi sampel itu dalam bentuk stochastic seperti berikut :
Yi = a + bXi + ei
dimana ei adalah residual dan ei merupakan penduga terhadap ui.
Akhirnya timbul pertanyaan, bagaimana membentuk persamaan regresi populasi sehingga a sedekat mungkin dengan A (yang sesungguhnya) dan b sedekat mungkin dengan B (yang sesungguhnya)?
Telah disebutkan bahwa dalam analisis regresi tujuan utamanya adalah menduga fungsi regresi populasi berdasar fungsi sampel setepat mungkin. Sampai saat ini ada banyak metode untuk menyusun persamaan regresi sampel, misalnya free hand, least squares dan maximum likelihood. Dalam analisis regresi metode yang paling banyak digunakan adalah metode least squares. Berikut adalah penurunan rumus dari regresi populasi ke metode least squares.
\dpi{120} \epsilon (Y|X)=A+BX_{i}
Dimulai dari rumus di atas, maka dimulailah pencarian metode least squares. Metode least squares merupakan metode yang memiliki jumlah kuadrat kesalahan paling kecil. Artinya meminimumkan :
Karena jumlah residual adalah fungsi dari a dan b, dengan proses diferensiasi dihasilkan rumus berikut :
dimana n banyaknya observasi.
Bila persamaan regresi sampel telah dibentuk maka kurva yang sesuai dapat dibuat lebih mudah. Penduga yang diperoleh melalui prinsip least squares dinamakan penduga least squares.
Sementara itu garis regresi sampelnya memiliki ciri-ciri:
- melalui rata-rata X dan Y yang diperoleh dari sampel, atau melalui titik
.
- rata-rata nilai residu sama dengan 0 karena
.
Contoh: suatu sampel random sebanyak 10 keluarga bertujuan untuk melihat hubungan antara pengeluaran konsumsi (Y) dengan pendapatan keluarga (Xi). Hasil pengamatan itu dapat dilihat pada tabel di bawah ini.
Kelompok (Y) | Pendapatan (X) | XY | |
70 65 90 95 110 115 120 140 155 150 | 80 100 120 140 160 180 200 220 240 260 | 5600 6500 10800 13300 17600 20700 24000 30800 37200 39000 | 6400 |
sumber: Mulyono, Sri. Statistika Untuk Ekonomi. Edisi kedua. LPFEUI. 2003.
Jawab:
sehingga persamaan regresi sampelnya :
ini berarti bahwa jika X naik satu satuan maka Y akan bertambah sebesar 0,5091. Bila b = 0 berarti tak ada hubungan antara Y dan X dan regresi sampelnya merupakan garis horizontal. Garis regresi sampel dapat digambarkan dengan mengambil dua pasang titik (X,Y) secara sembarang.

Tidak ada komentar:
Posting Komentar