Chi Square Goodness-Of-Fit Test

Banyak penelitian yang didesain untuk mengetahui jumlah subyek, obyek atau jawaban (response) yang jatuh pada berbagai kategori. Misalkan anak-anak dapat dikategorikan menurut frekuensi jenis permainan yang sering dimainkan, hipotesis penelitiannya adalah jenis permainan ini akan berbeda frekuensinya dengan cara tertentu. Orang dapat dikategorikan menurut apakah mereka "lebih suka" atau "menolak" suatu opini sehingga sipeneliti dapat menguji hipotesis bahwa response ini akan berbeda dalam frekuensinya.

Uji Chi-Square cocok untuk menganalisis data seperti di atas. Jumlah kategori dapat dua atau lebih. Teknik yang digunakan adalah goodness-of-fit dan dapat digunakan untuk menguji apakah terdapat perbedaan signifikan antara jumlah obyek atau response yang diobservasi yang jatuh pada setiap kategori dan jumlah obyek yang diharapkan (expected) berdasarkan pada hipotesis nol. Jadi uji goodness-of-fit menilai tingkat kesesuaian (correspondence) antara observed dan expected observation dalam setiap kategori.

Untuk membandingkan antara frekuensi observasi dengan frekuensi grup yang diharapkan (expected), kita harus mampu menyatakan frekuensi yang diharapkan. Hipotesis no H0 menyatakan bahwa proporsi obyek masuk dalam setiap kategori pada populasi yang diasumsikan. Dari hipotesis nol, kita dapat menarik kesimpulan frekuensi seperti apa yang kita harapkan. Teknik Chi-Square memberikan probabilitas bahwa frekuensi yang diobservasi telah dipilih dari populasi dengan nilai expected tertentu. Hipotesis nol dapat diuji dengan statistik sebagai berikut :

x^{2}=\sum_{i=1}^{k}\frac{\left (O_{i}-E_{i} \right )^{2}}{E_{i}} (persamaan 3)

Dimana :
Oi = jumlah observed cases dalam ke-i kategori
Ei = jumlah expected cases dalam ke-i kategori ketika H0 benar
k = jumlah kategori

Jika kesesuaian antara observed dan expected frekuensi dekat, maka perbedaan antara (Oi-Ei) akan kecil dan konsekuensinya, x² akan kecil. Namun demikian jika perbedaannya besar, maka x² juga akan besar. Semakin besar nilai x², maka semakin kecil prbabilitas bahwa observasi frekuensi berasal dari populasi dimana H0 dan expected frekuensi didasarkan. Walaupun (persamaan 3) berguna untuk memahami x², tetapi memerlukan perhitungan yang banyak, rumus yang lebih sederhana untuk menghitung x² sebagai berikut :

x^{2}=\sum_{i=1}^{k}\frac{O_{i}^{2}}{E_{i}}-N

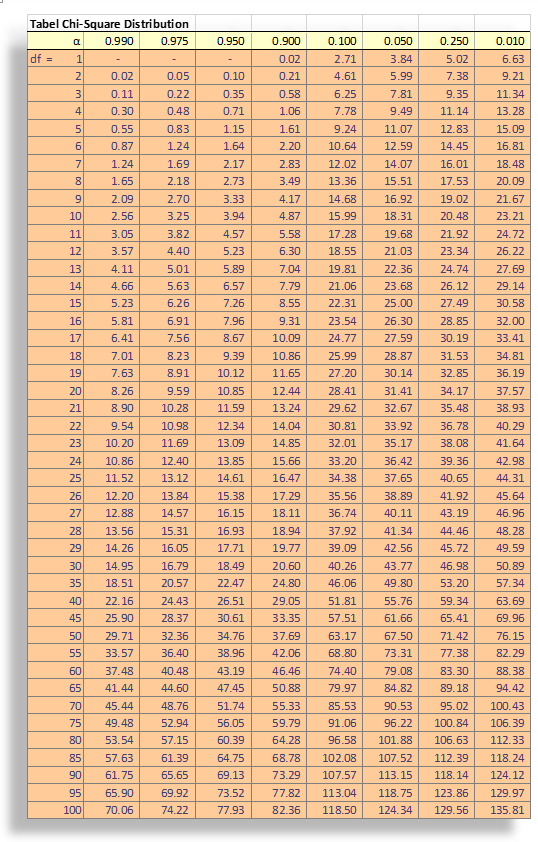
N adalah jumlah observasi. Sampling distribusi x² pada H0 seperti dihitung dari rumus (persamaan 3) mengikuti distribusi Chi-square dengan degree of freedom (df) = k-1. Tabel dsampling distribution Chi-Square dengan probabilitas yang berkaitan dengan nilai tertentu. Pada setiap atas kolom tabel Chi-square berisi probabilitas accurrence dari nilai Ch-square jika H0 benar. Nilai dalam kolom adalah nilai Chi-square. Misalkan dengan df=1 dan H0 adalah benar, maka probabilitas observasi nilai Chi-square sebesar 3.84 (atau lebih besar) adalah 0.05. Pada umumnya untuk kasus satu sampel goodness-of-fit test, ketika H0 menspesifikasi Ei's, df = k-1, dimana k adalah jumlah kategori dalam klasifikasi. Untuk menjelaskan uji statistik ini kita gunakan kasus dibawah ini.

Para penggemar balap kuda sering menyatakan bahwa dalam balapan kuda pada track berbentuk lingkaran, kuda pada posisi start tertentu akan mendapatkan keuntungan secara signifikan. Posisi kuda pada saat start terdiri dari posisi 1 adalah posisi paling dekat dengan rail pada inside track, sedangkan posisi 8 ada di lingkaran paling luar dan terjauh dari rail track untuk pacuan kuda yang diikuti 8 ekor kuda. Kita ingin menguji pengaruh posisi start dengan menganalisis hasil pacuan kuda sesuai dengan posisi start mereka selama sebulan musim pacuan kuda pada track berbentuk lingkaran. Hasil pengamatan dapat dilihat pada tabel di bawah ini.

Tabel Hasil Pengamatan Pacuan Kuda, Jumlah Menang dan Posisi Start Kuda

Posisi Start	1	2	3	4	5	6	7	8	Total
Jumlah Menang	29	19	18	25	17	10	15	11	144
Expected	18	18	18	18	18	18	18	18

Langkah analisis

1. Hipotesis nol. H0 : tidak ada perbedaan dalam jumlah pemenang yang diharapkan dengan nomor sesuai dengan nomor start, dan jika ada perbedaan observasi semata-mata karena variabel acak yang diharapkan dari sampel random yang diambil dari distribusi uniform.
   Hipotesis alternatif. H1 : frekuensi teoritis semua tidak sama.
2. Uji statistik. Oleh karena kita membandingkan data dari satu sampel dengan populasi yang telah diasumsikan terlebih dahulu, maka uji chi-square goodness-of-fit test adalah yang cocok untuk analisis ini. Chi-square dipilih karena hipotesis yang diuji membandingkan frekuensi yang diobservasi dengan frekuensi yang diharapkan dalam kategori diskrit. Dalam kasus ini ke delapan nomor start merupakan kategori.
3. Tingkat signifikansi. Tingkat signifikansi alpha =0.01 dan N = 144 jumlah pemendang daam 18 hari pacuan kuda.
4. Sampling distribution statistik x² dihitung dari (persamaan 2) yang diikuti distribusi Chi-square dengan df = k-1 = 8-1 = 7.
5. Daerah penolakan Ho akan ditolak jika nilai observasi x² sedemikian rupa sehingga probabilitas yang berkaitan dengan nilai hitung pada H0 untuk df = 7 adalah < 0.01.
6. Keputusan. Pada tabel di atas memberikan data bahwa ada 29 pemenang untuk kuda dengan start no.1, dengan H0 hanya 18 pemenang yang diharapkan. Sedangkan untuk kuda dengan start no.8 ada 18 pemenang, dengan H0 hanya 18 pemenang yang diharapkan. Dari tabel di atas maka x² dapat dihitung sebagai berikut :

x^{2}=\sum_{i=1}^{8}\frac{\left (O_{i}|E_{i} \right )^{2}}{E_{i}}
=\frac{\left (29|18 \right )^{2}}{18}+\frac{\left (19|18 \right )^{2}}{18}+\frac{\left (18|18 \right )^{2}}{18}+\frac{\left (25|18 \right )^{2}}{18}+\frac{\left (17|18 \right )^{2}}{18}+\frac{\left (10|18 \right )^{2}}{18}+\frac{\left (15|18 \right )^{2}}{18}+\frac{\left (11|18 \right )^{2}}{18}=16.3

Tabel Chi-square menunjukkan bahwa P[x^{2}\geqslant 16.3] dengan df = 7 memiliki probabilitas antara p = 0.05 dan p = 0.02, jadi 0.05 > p < 0.02. Oleh karena probabilitasnya lebih besar dari alpha = 0.01, maka kita tidak dapat menolak H0. Namun demikian, jika tingkat signifikansi alpha = 0.05, maka H0 dapat ditolak. Kelihatannya kita memerlukan lebih banyak data sebelum keputusan definitip dapat dilakukan terhadap H1.

Langkah analisis

1. Buat file dengan nama Test Chi-Square dengan 2 variabel yaitu observasi dan pemenang. Pada variabel observasi isikan no. urut 1 s.d 144 dan pada variabel pemenang isikan pemenang 1 ada 29 observasi, pemenang 2 ada 19 observasi, pemenang 3 ada 18 observasi, pemenang 4 ada 25 observasi, pemenang 5 ada 17 observasi, pemenang 6 ada 10 observasi, pemenang 7 ada 15 observasi, dan pemenang 8 ada 11 observasi.
2. Dari menu SPSS pilih menu Analyze kemudian pilih Non Parametric Tests lalu pilih Legacy Dialogs dan pilih Chi-Square Test.
3. Tampak dilayar tampilan windows Chi-Square Tests.
4. Isikan pada Test Variable List dengan variable Pemenang, keterangan lainnya biarkan seperti Expected Range dengan Get from data, dan Expected Values dengan All Categories Equal (default SPSS).
5. Terakhir tekan OK

Interpretasi Output SPSS

Tampilan SPSS menunjukkan nilai observasi maupun ekspektasi dari jumlah pemenang dengan no start 1 sampai 8. Nilai statistik Chi-Square sebesar 16.333 dengan df = 7 menunjukkan probabilitas sebesar 0.022 dan nilai ini lebih besar dari alpha = 0.01 sehingga dapat disimpulkan bahwa kita tidak dapat menolak H0.