Uji Binomial

Ada banyak populasi yang hanya terdiri dari dua kelompok. Sebagai misal laki-laki dan wanita, buta huruf dan melek huruf, anggota dan buan anggota, kawin dan bujangan. Untuk kasus semacam ini, semua kemungkinan observasi dari populasi akan jatuh ke dalam dua kategori diskrit. Populasi semacam ini disebut binary population atau dichotomous population.

Misalkan sebuah populasi terdiri dari dua kategori. Setiap observasi (X) sampel dari populasi akan memberikan nilai 1 dan 0. Probabilitas mengambil sampel sebuah obyek dari kategori pertama adalah p dan probabilitas mengambil obyek dari kategori lainnya adalah q = 1-p, jadi : P[X=1] = P dan P[X=0] = 1-p = q.

Diasumsikan juga bahwa setiap probabilitas adalah konstan untuk jumlah obyek yang observasi. Walaupun nilai p dapat bervariasi dari populasi ke populasi, tetapi nilai p akan tetap untuk satu populasi. Walaupun kita tahu nilai p untuk beberapa populasi, tetapi kita tidak dapat mengharapan bahwa observasi dengan random dari populasi akan berisi proporsi p dan 1-p untuk setiap dua kategori. Misalkan kita mungkin tahu dari catatan resmi pemerintah bahwa pemilih di satu tempat terbagi merata antara partai Republik dan partai Demokrat. Dengan random sampel terhadap pemilih yang terdaftar di satu lokasi terdiri dari 47% Demokrat dan 53% adalah Republik. Perbedaan antara observasi dan nilai populasinya terjadi secara "acak" atau random fluktuasi dalam observasi.

Distribusi binomial digunakan untuk menentukan probabilitas outcome yang akan kita dapat jika kita mengambil sampel dari populasi binomial. Jika hipotesis kita adalah H0: p = po, kita dapat menghitung probabilitas berbagai outcome ketika diasumsikan bahwa H0 adalah benar. Uji ini akan menyatakan kepada kita adalah cukup alasan untuk mempercayai bahwa proporsi (frekuensi) dua kategori di dalam sampel kita dapat ditarik dari populasi dengan nilai hipotesis po dan 1-po. Untuk memudahkan dalam mendiskusikan distribusi binomial, kita nyatakan outcome X=1 sebagai "sukses" dan outcome X=0 sebagai "gagal". Untuk seri sejumlah N observasi adalah :

Y = \sum_{i=1}^{N}X_{i}
Jumlah "sukses" atau jumlah outcome jenis X = 1.

Dalam sampel dengan ukuran N, probabilitas mendapatkan k obyek dalam satu kategori dan N-k obyek dalam kategori lain dapat dinyatakan sebagai berikut:

P[Y=k]=\binom{N}{k}p^{k}q^{N-k}
dimana k = 0., 1, ... N (persamaan 1)
p = proporsi observasi yang diharapkan jika X=1.
q = proporsi observasi yang diharapkan jika X=0.
\binom{N}{k}=\frac{N!}{k!(N-k)!}

Contoh sederhana berikut ini akan menjelaskan (persamaan 1) di atas. Misalkan kita melempar sebuah dadu lima kali. Berapakah probabilitas bahwa dua lemparan akan memberikan angka enam? Dalam kasus ini Y adalah variabel random (outcome lima kali lemparan dadu). N = jumlah lemparan (5), k = jumlah observasi angka enam (2), p = proporsi yang diharapkan adalah enam (1/6), dan q = 1-1/6, maka probabilitas bahwa dua kali lemparan menghasilkan angka enam adalah :

P[Y=k]=\binom{N}{k}p^{k}(1-p)^{N-k}
P[Y=2]=\binom{5!}{2!3!}(1/6)^{2}(5/6)^{3} = 0.16

Aplikasi dari rumus di atas menunjukkan bahwa probabilitas mendapatkan dua angka "enam" ketika melempar dadu lima kali adalah p = 0.16.

Jika kita ingin menguji hipotesis, pertanyaan yang diajukan bukan, "berapakah probabilitas mendapatkan nilai yang kita observasi?" tetapi kita biasanya mengajukan pertanyaan "berapakah probabilitas mendapatkan nilai ekstrim atau lebih ekstrim daripada nilai observasi, ketika kita mengasumsikan bahwa data diambil dari proses tertentu?". Untuk menjawab pertanyaan seperti ini probabilitasnya dapat dirumuskan sebagai berikut :

P[Y\geqslant k]=\sum_{i=k}^{N}\binom{N}{i}p^{i}q^{N-i} (persamaan 2)

Dengan kata lain, kita menjumlahkan probabilitas outcome yang terobservasi dengan probabilitas outcome yang lebih ekstrim.

Misalkan kita ingin mengetahui probabilitas mendapatkan dua atau lebih sedikit angka enam jika sebuah dadu dilempar lima kali. Disini N = 5, k = 2, p = 1/6 dan q = 5/6. Probabilitas mendapatkan dua atau lebih sedikit angka enam P[Y<2]. Dari (persamaan 1) probabilitas mendapatkan nol angka enam adalah P[Y=0], probabilitas mendapatkan satu angka enam adalah P[Y=1] dan seterusnya. Menggunakan (persamaan 2) kita dapatkan :

P[Y<2] = P[Y=0] + P[y=1] + P[Y=2]
P[Y=0]=\frac{5!}{0!5!}\left (\frac{1}{6} \right )^{0}\left (\frac{5}{6} \right )^{0}=0.40
P[Y=1]=\frac{5!}{1!4!}\left (\frac{1}{6} \right )^{1}\left (\frac{5}{6} \right )^{4}=0.40
P[Y=2]=\frac{5!}{2!3!}\left (\frac{1}{6} \right )^{2}\left (\frac{5}{6} \right )^{3}=0.16
Jadi P[Y=<2] = P[Y=0] + P[Y=1] + P[Y=2] = 0.40 + 0.40 + 0.16 = 0.96

Kita dapat menentukan bahwa probabilitas H0 (asumsi pelemparan dadu fair) mendapatkan dua kurang dari dua angka enam ketika dadu dilempar lima kali adalah p=0.96.

Sampel Kecil

Pada kasus satu sampel, ketika kategori binari digunakan, hipotesis secara umum dinyatakan H0:P=1/2. Tabel di bawah ini memberikan nilai probabilitas satu sisi (one tail) terjadinya berbagai nilai ekstrim k dengan hipotesis H0:p=1/2. Jika menggunakan tabel di bawah ini, k sama dengan smaller observed frequencies. Tabel ini berguna jika N<35. Walaupun (persamaan 2) dapat digunakan, tetapi tabel lebih mudah dipakai. Cara menggunakan tabel. Misalkan kita mengobservasi 7 "sukses" dan 3 "gagal" disini N = 10, k = 7. Tabel dibawah ini menunjukkan probabilitas satu arah (one tail) terjadinya Y<3 pada kondisi H0:P=/12, maka P[Y=7]=0.172.

Kasus berikut ini memberikan ilustrasi penggunaan uji binomial dimana H0:p=1/2

Dalam studi pengaruh stress, seorang peneliti memberikan pelajaran kepada 18 orang mahasiswa 2 metode yang berbeda untuk membuat tali simpul. Setengah dari subyek (dipilih secara random dari 18 mahasiswa) mempelajari metode A lebih dahulu baru metode B, dan setengah subyek yang lain mempelajari metode B lebih dahulu baru metode A. Kemudian tengah malam, setelah 4 jam mereka menempuh ujian final setiap subyek diminta untuk membuat tali simpul. Prediksinya adalah stress akan mengakibatkan kemunduran (regresi) atau subyek akan kembali kepada metode pertama mereka pelajari dalam membuat tali simpul. Setiap subyek dikategorikan sesuai dengan apakah subyek menggunakan metode yang dipelajari pertama atau metode yang dipelajari kedua ketika diminta untuk membuat tali simpul pada kondisi stress.

Langkah Analisis

1. Hipotesis nol, H0:p=q=1/2, yaitu tidak ada perbedaan probabilitas menggunakan metode pertama pada kondisi stress (p) dan probabilitas menggunakan metode kedua pada kondisi stress (q). Sedangkan hipotesis alternatifnya H1:p>q, yaitu pada kondisi stress, probabilitas menggunakan metode pertama lebih besar daripada probabilitas menggunakan metode pertama lebih besar daripada probabilitas menggunakan metode kedua.
2. Uji statistik. Uji binomial dipilih oleh karena data adalah dua kategori diskrit dan desain penelitian adalah uji satu sampel. Oleh karena metode A dan B diberikan secara randam sebagai metode pertama dan kedua yang harus dipelajari, maka tidak ada alasan bahwa metode yang pertama dipelajari lebih disukai daripada metode kedua yang dipelajari pada H0:p=q=1/2.
3. Tingkat signifikansi. Tingkat signifikansi dipilih a=0.01 dan N adalah jumlah kasus = 18.
4. Sampling distribution. Sampling distribution diberikan oleh (persamaan 2). Namun demikian jika N<35, dab p=q=1/2, maka tabel dibawah ini memberikan probabilitas terjadinya nilai yang diobservasi sekecil k pada H0.
5. Daerah penolakan. Daerah penolakan terdiri dari semua nilai Y (dimana Y adalah jumlah subyek yang menggunakan metode kedua pada kondisi stress) yang nilainya begitu kecil sehingga probabilitas terjadinya pada kondisi H0 adalah sama atau lebih kecil dari alpha = 0.01. Oleh karena arah perbedaan telah ditentukan lebih dahulu maka digunakan uji satu sisi (one tail).
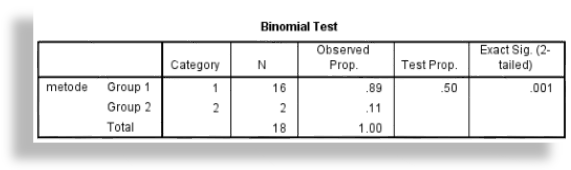
6. Keputusan. Dalam eksperimen, dari 18 subyek yang menggunakan metode kedua untuk membuat tali simpul pada kondisi stress ada 2 orang. Data eksperimen dapat dilihat pada tabel dibawah ini. Dalam kasus ini N adalah jumlah observasi independen = 18, k frekuensi terkecil = 2. tabel di bawah ini menunjukkan N= = 18, probabilitas yang berkaitan dengan K<2 adalah 0.001, probabilitas ini lebih kecil dari alpha = 0.01, jadi keputusannya menolak H0 dan menerima H1 jadi orang pada kondisi stress akan kembali mengunakan metode membuat tali simpul yang pertama kali mereka pelajari.

Aplikasi uji binomial dengan program SPSS. Data yang akan dianalisis ditabulasikan dalam prgram excel dengan format tabel 2x2. Metode yang dipilih untuk membuat tali simpul dikategorikan menjadi 1 untuk metode yang pertama kali dipelajari dan 2 untuk metode yang kedua dipelajari. Data ini disimpan dalam file binomial.xls

1. Buat data binomial dengan variabel Observasi dan Metode.
2. Dari menu SPSS pilih menu Analyze kemudian pilih Non Parametric Tests lalu pilih Legacy Dialogs dan pilih Binomial.
3. Tampak dilayar tampilan windows Binomial Tests
4. Isikan pada Test Variable List dengan variable Metode, keterangan lainnya biarkan seperti Test Proportion by Default adalah 0.50 (proporsi ini dapat dirubah sesuai dengan yang kita kehendaki) dan Define Dichotomy isikan get from data (default SPSS).
5. Oleh karena variabel Metode merupakan variabel dikotomi (berisi dua macam nilai), maka pada define dichotomy kita pilih get from data. Kasus yang mempunyai nilai kategori kecil dalam hal ini 1 dimasukkan pada grup pertama (menggunakan proporsi p), dan kasus yang mempunyai nilai kategori besar dalam hal ini 2 dimasukkan sebagai grup kedua (menggunakan proporsi q=1-p). Sedangkan apabila variabel bukan dikotomi, maka harus menggunakan cut point. Kasus yang nilainya lebih kecil atau sama dengan cut point akan dimasukkan pada grup pertama dan sisanya pada grup kedua.
6. Abaikan yang lain dan tekan OK
   
   

Interpretasi output SPSS

Tampilan output SPSS menunjukkan bahwa frekuensi yang memilih metode 1 dan 16 dengan observed proportion 0.898 dan memilih metode 2 ada 2 orang dengan observed proportion 0.11. Proporsi pengujian adalah 0.50 dengan tingkat probabilitas signifikansi 0.001 (two tail) atau 0.0005 (one tail). Probabilitas signifikansi ini jauh dibawah alpha = 0.01. Jadi dapat disimpulkan bahwa probabilitas orang dalam kondisi stress cenderung memilih metode membuat tali simpul yang pertama kali mereka pelajari.

Sampel Besar

Tabel D tidak dapat digunakan jika jumlah sampel N > 35. Sungguhpun demikian dapat ditunjukkan bahwa semakin besar N, maka distribusi binomial cenderung mendekati distribusi normal. Kecendrungan mendekati distribusi normal ini kuat jika p mendekati 1/2 tetapi akan semakin melambat jika p mendekati 0 dan 1. Jadi semakin besar kesenjangan antara p dan q dan N harus berjumlah besar, maka distribusi binomial mendekati distribusi normal. Sampling distribution Y akan mendekati normal dengan mean (rata-rata) Np dan variance Npq sehingga hhipotesis H0 dapat diuji dengan rumus :

z=\frac{x-\mu _{x}}{\sigma _{x}}=\frac{Y-Np}{\sqrt{Npq}}

Dimana nilai z mendekati distribusi normal dengan mean 0 dan standar deviasi 1. Tingkat signifikansi nilai z dapat ditentukan dengan Tabel A yang memberikan probabilitas satu sisi (one tail).