Seperti telah dijelaskan pada postingan yang lalu bahwa model regresi memiliki fungsi linear dalam parameternya, walaupun variabelnya dapat linear maupun non-linear. Pada kesempatan ini akan dijelaskan beberapa model regresi yang memiliki variabel non-linear tetapi memiliki parameter linear. Model regresi itu antara lain : The Log Linear Models, Semi Log Models, Reciprocal Models dan The Logaritmic Reciprocal Models.
Mengukur Elastisitas dengan Log-Linear Models
Berikut ini adalah model regresi exponensial yang diwujudkan dalam persamaan sebagai berikut :
Y_{i}=\beta _{i}X_{i}^{\beta 2}e^{ui}Persamaan ini dapat ditulis dalam bentuk logaritma natural menjadi :
LnY_{i}=Ln\beta _{1}+\beta _{2}LnX _{i}+uiDimana Ln = logaritma natural (log berbasis e, dimana e = 2.718), jika LnY_{i}=Ln\beta _{1}=\alpha, maka persamaan di atas, dapat ditulis menjadi :
LnY_{i}=\alpha+\beta _{2}LnX _{i}+uiModel regresi ini memiliki linear parameter \alpha dan \beta _{2} dan linear variabel logaritma Y dan X sehingga dapat diestimasi dengan Ordinary Least Squares (OLS). Oleh karena linearitas maka model regresi ini sering disebut dengan log-log, double-log, atau log-linear model.
Jika asumsi klasik model regresi linear dipenuhi, maka parameter persamaan terakhir di atas dapat diestimasi dengan OLS dengan cara :
Y_{i}^{*}=\alpha+\beta _{2}X _{i}^{*}+uiDimana Y_{i}^{*}=LnY _{i} dan X_{i}^{*}=LnX _{i}
Salah satu yang menarik dari model log-log model ini adalah slope (kemiringan, garis diagonal) koefisien \beta_{2} mengukur elastisitas Y terhadap X, yaitu besarnya perubahan dalam Y yang disebabkan oleh besarnya perubahan X. Model ini mengasumsikan bahwa koefisien elastisitas antara Y dan X adalah konstan (tetap) atau constant elasticity model.
Untuk memberikan contoh log-log model ini kita gunakan data file log-lin.xls yang berisi data total personal consumption expenditure (PCEXP), expenditure on durable goods (EXDUR), expenditure on non-durable goods (EXPNONDUR) dan expenditure on services (EXPSER) semua diukur dengan billion dollar tahun 1992. Misalkan kita ingin mengetahui elastisitas pengeluaran untuk barang durable terhadap pengeluaran konsumsi individu. Hal ini dapat ditulis persamaan regresinya menjadi :
LnEXDUR_{t}=\alpha+\beta _{2}LnPCEXP_{t}+uiLangkah analisis
- Buka file log-lin.xls
- Dari menu utama SPSS pilih Transform dan Compute.
- Tranformasikan variabel EXPDUR dan PCEXP ke dalam bentuk logaritma natural.
- Dari menu utama SPSS pilih Regression, lalu pilih submenu Linear.
- Isikan pada kotak Dependent variabel LnEXPDUR.
- Isikan pada kotak Independent variabel LnPCEXP.
- Abaikan yang lain dan tekan OK
Interpretasi Output SPSS
Hasil output SPSS menunjukkan bahwa elastisitas pengeluaran barang durable terhadap pengeluaran konsumsi sekitar 1.9 yang berarti jika total pengeluaran konsumsi naik 1%, maka rata-rata pengeluaran untuk barang durable akan naik sebesar 1.9%. Jadi pengeluaran untuk barang durable sangat responsif terhadap perubahan pengeluaran konsumsi. Koefisien determinasi dari model ini ditunjukkan oleh besarnya adjusted R2 yaitu sebesar 0.984 yang berarti variabilitas pengeluaran untuk barang durable yang dapat dijelaskan oleh variabilitas pengeluaran konsumsi sebesar 98.4%.
Mengukur Tingkat Pertumbuhan : Log-Linear Models
Ekonom, pengusaha dan pemerintah sering berkepentingan dengan pengukuran tingkat pertumbuhan suatu variabel ekonomi seperti Penduduk, GNP, Supply uang, Employment, Produktivitas dan Defisit perdagangan
Misalkan berdasarkan data file Log-lin.xls, ingin mengetahui tingkat pertumbuhan pengeluaran konsumsi untuk barang jasa (EXPSER). Yt merupakan pengeluaran real barang jasa pada waktu t dan Yo adalah nilai awal pengeluaran barang jasa (nilai akhir tahun 1992-IV). Berdasarkan pada persamaan compound interest (bunga majemuk) dapat dituluskan :
Y_{t}=Y _{o}(1+r)^{t}Dimana r adalah nilai compound tingkat pertumbuhan Y. Persamaan ini dapat dirubah dalam logaritma natural menjadi :
LnY_{t}=LnY _{o}+tLn(1+r)Dengan menganggap \beta_{1}=LnY _{o} dan \beta_{2}=Ln(1+r), maka persamaan dapat disederhanakan menjadi :
LnY_{t}=\beta _{1} + \beta _{2} + utModel regresi ini merupakan regresi linear pada parameter \beta_{1} dan \beta_{2}, bedanya pada variabel dependen berbentuk logaritma sedangkan variabel independen merupakan waktu (t) yang mempunyai nilai 1, 2, 3 dst. Model ini sering disebut semi-log model karena hanya ada satu variabel dalam bentuk logaritma yang variabel dependen dan disebut juga log-lin model.
Pada model ini slope koefisien mengukur proporsi konstan atau perubahan relatif Y terhadap perubahan absolut nilai t atau :
\beta _{2}=\frac{Perubahan relatif variabel dependen}{Perubahan absolut variabel independen}Jika kita mengalikan perubahan relatif Y dengan angka 100, maka akan memberikan perubahan persentase atau tingkat pertumbuhan. Dalam literatur \beta_{2} dikenal dengan semi elastisitas Y terhadap X.
Langkah analisis
- Buka file log-lin.xls
- Dari menu utama SPSS pilih Transform dan Compute.
- Tranformasikan variabel EXPSER dalam bentuk logaritma natural.
- Dari menu utama SPSS pilih Regression, lalu pilih submenu Linear.
- Isikan pada kotak Dependent variabel LnEXPSER.
- Isikan pada kotak Independent t (tahun observasi).
- Abaikan yang lain dan tekan OK
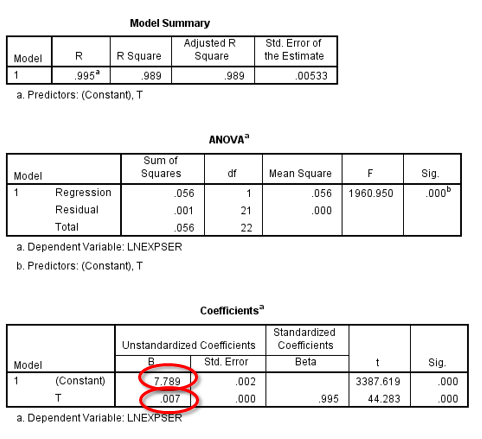
Interpretasi Output SPSS
Interpretasi dari model ini adalah selama periode kuartalan dari tahun 1993:1 sampai 1998:3 pengeluaran untuk barang jasa mengalami kenaikan (per kuartal) dengan tingkat kenaikan 7%. Secara kasar ini sama dengan tingkat pertumbuhan per tahun 2.97%. Oleh karena 7.789 = Ln EXPSER awal periode dengan melakukan antilog pada angka ini didapat nilai 2413.90 (milyar dollar) yang merupakan nilai awal pengeluaran barang jasa atau nilai EXPSER.
Lin-Log Model
Kita mungkin tertarik untuk menghitung perubahan absolut Y terhadap persentase perubahan X (perubahan relatif), model regresi seperti ini disebut Lin-Log model karena variabel independen dalam bentuk logaritma dan persamaannya sebagai berikut :
Y_{i}=\beta _{i} + \beta _{2} Ln X _{i} + {ui}Interpretasi terhadap slope koefisien \beta _{2} seperti biasa menjadi :
\beta _{2}=\frac{Perubahan absolut Y}{Perubahan relatif X}
Secara simbolik dapat dituliskan.
\beta _{2}=\frac{\Delta Y}{\Delta X/X}=\beta _{2}(\Delta X/X)
Simbol \Delta menandakan perubahan dalam nilai kecil. Persamaan ini menyatakan bahwa perubahan absolut dalam Y(\Delta Y) sama dengan slope dikalikan perubahan relatif X. Jika perubahan relatif X dikalikan 100, maka akan memberikan perubahan absolut Y terhadap perubahan persentase X. Jadi jika (\Delta X/X) berubah dengan 0.01 unit atau 1%, maka perubahan absolut Y adalah 0.01 \beta _{2}.
Dalam aplikasi misalkan kita mendapatkan nilai \beta _{2} = 500, maka perubahan absolut Y adalah (0.01) (500) = 5. Oleh karena itu jika model regresi lin-log akan diestimasi dengan OLS jangan lupa mengalikan nilai slope koefisien dengan angka 0.01 atau dibagi dengan 100. Hal ini penting agar interpretasi tidak menyesatkan.
Kapan model lin-log ini digunakan, penerapan model ini salah satunya digunakan untuk menghitung model pengeluaran Engel, nama seorang ahli statistik Jerman Ernst Engel (1821-1896). Engel menyatakan bahwa "total pengeluaran untuk makanan cenderung meningkat secara aritmatik, sedangkan total pengeluaran meningkat secara geometrik".
Untuk memberikan gambaran kita akan gunakan data file lin-log.xls yang berisi variabel Total pengeluaran untuk makanan dan variabel Total pengeluaran terhadap total pengeluaran makanan dengan persamaan regresi FoodEXP =\beta _{i} + \beta _{2} LnEXP + {ui}.
Langkah analisis
- Buka file log-lin.xls
- Dari menu utama SPSS pilih Transform dan Compute.
- Tranformasikan variabel FoodEXP dan totalexp ke dalam bentuk logaritma natural.
- Dari menu utama SPSS pilih Regression, lalu pilih submenu Linear.
- Isikan pada kotak Dependent variabel FoodEXP.
- Isikan pada kotak Independent variabel LnEXP.
- Abaikan yang lain dan tekan OK
Interpretasi Output SPSS
Interpretasi terhadap hasil regresi menunjukkan bahwa slope koefisien sebesar 223 yang berarti kenaikan total pengeluaran untuk makanan 1%, maka rata-rata sekitar 2.57 rupee kenaikan pengeluaran untuk makanan bagi 55 keluarga dalam sampel(ingat slope koefisien dibagi 100).
Model Reciprocal
Berikut adalah model persamaan regresi reciprocal :
Y_{i}=\beta _{i} + \beta _{2} (1/X _{i}) + utWalaupun model ini non-linear dalam variabel X karena nilai X reciprocal (terbalik), tetapi model ini linear dalam parameter \beta_{1} dan \beta_{2}. Oleh karena itu disebut model regresi linear. Model ini mempunyai makna jika X meningkat tak terhingga (indefinitely), maka \beta_{2} (1/X _{i}) mendekati nol (catatan \beta_{2} konstan) dan Y mendekati limit atau nilai asymptote \beta_{1}. Bentuk kurva model reciprocal dapat dilihat dari plot data file reciproc.xls yang berisi data crossection 64 negara untuk Mortalitas anak (CM), persentase melek huruf wanita (FLFP), GNP per capita (GGNP) dan tingkat fertilitas total (TFR). Gambar grafik berikut ini adalah plot Mortalitas anak dan GNP per capita.
Dari grafik ini terlihat bahwa kenaikan GNP per kapita akan menurunkan mortalitas anak karena banyak orang mampu mengeluarkan biaya untuk kesehatan dengan asumsi variabel lain konstan. Pada grafik tampak bahwa hubungannya tidaklah garis lurus. Kenaikan GNP pada awalnya terjadi penurunan mortalitas dramatis, tetapi penurunannya semakin kecil dengan kenaikan GNP per kapita. Jika kita mencoba menggambarkan hal ini dengan persamaan regresi model reciprocal persamaannya sebagai berikut :
CM_{i}=\beta _{i} + \beta _{2} (1/PGNP _{i}) + uiLangkah analisis
- Buka file reciproc.xls
- Dari menu utama SPSS pilih Transform dan Compute.
- Tranformasikan variabel PGNP menjadi bentuk 1/PGNP.
- Dari menu utama SPSS pilih Regression, lalu pilih submenu Linear.
- Isikan pada kotak Dependent variabel CM.
- Isikan pada kotak Independent variabel 1/PGNP.
- Abaikan yang lain dan tekan OK
Interpretasi Output SPSS
Interpretasi hasil regresi ini adalah dengan kenaikan GNP per capita tak terhingga, maka mortalitas anak (CM) akan mendekati nilai asymptote sekitar 82 kematian per seribu. Nilai positif koefisien (1/PGNP) mempunyai implikasi bahwa tingkat perubahan CM terhadap PGNP adalah negatif.
Pemilihan Bentuk Fungsional
Bentuk regresi fungsional mana yang harus dipilih dapat dilakukan dengan memperhatikan beberapa hal berikut ini :
- Melihat teori yang mendasarinya (misalkan kurve philip) maka harus memilih bentuk regresi reciprocal.
- Adalah praktek yang baik menentukan tingkat perubahan (slope) variabel dependen terhadap variabel independen, begitu juga menentukan elastisitas variabel dependen terhadap variabel independen. Dari berbagai model berikut ini diberikan rumus menghitung slope dan koefisien elastisitas dari berbagai model.
Model-model Regresi Fungsional
Model Persamaan Slope
\frac{dY}{dX}
Elastisitas
\frac{dY}{dX}\frac{X}{Y}
Linear Y=\beta _{1}+\beta _{2}X \beta _{2} \beta _{2}(X/Y) Log-Linear LnY=\beta _{1}+\beta _{2}LnX \beta _{2}(Y/X) \beta _{2} Log-lin LnY=\beta _{1}+\beta _{2}X \beta _{2}(Y) \beta _{2}(X) Lin-log Y=\beta _{1}+\beta _{2}LnX \beta _{2}(1/X) \beta _{2}(1/Y) Reciprocal Y=\beta _{1}+\beta _{2}(1/X) -\beta _{2}(1/X ^{2}) -\beta _{2}(1/XY) - Koefisien dari model yang dipilh harus memenuhi ekspektasi apriori. Sebagai misal permintaan automobil sebagai fungsi harga dan variabel lainnya, maka kita akan berharap terhadap koefisien negatif untuk variabel harga.









Tidak ada komentar:
Posting Komentar