Uji McNemar Change cocok diaplikasikan untuk desain penelitian “sebelum dan sesudah” (“before and aftar”) yaitu masing-masing subyek bertindak sebagai kontrol dan pengukuran variabel menggunakan skala nominal atau ordinal. Uji ini dapat digunakan untuk menguji efektivitas suatu perlakuan tertentu (rapat, editorial surat kabar, pidato kampanye, kunjungan pribadi, dan seterusnya).
Untuk menguji signifikansi perubahan dari observasi data, kita menggunakan tabel frekuensi 2x2 yang menggambarkan jawaban pertama dan kedua dari individu yang sama. Contoh tabel frekuensi dapat dilihat pada tabel berikut ini.
| Sesudah | ||
| Sebelum | - | + |
| + | A | B |
| - | C | D |
Tanda + (plus) dan – (minus) digunakan untuk menunjukkan perbedaan jawaban. Perhatikan bahwa perubahan terhadap jawaban pertama dan kedua dapat dilihat pada kiri atas cell tabel (+ ke -) dan kana bawah cell tabel (- ke +). Angka pada tabel merupakan frekuensi terjadinya suatu outcome. Misalkan pada cell A menunjukkan jumlah individu yang jawabannya adalah + pada pengukuran awal dan jawaban – pada yang berubah dari jawaban – ke +. Cell B adalah frekuensi individu yang mempunyai jawaban tetap sama (+) pada pengukuran pertama maupun kedua, dan cell C merupakan jumlah individu yang mempunyai jawaban tetap sama (-) pada pengukuran pertama maupun kedua.
Jika A + D adalah jawaban orang yang jawabannya mengalami perubahan. Hipotesis nol adalah jumlah perubahan pada setiap arah adalah sama. Jadi jumlah orang yang jawabannya berubah A + D, kita berharap bahwa (A + D)/2 individu berubah dari + ke – dan (A + D)/2 individu berubah dari – ke +. Dengan kata lain, jika H0 benar, maka frekuensi yang diharapkan untuk setiap dua cell adalah (A + D)/2.
Dari rumus Chi-square kita mempunyai persamaan sebagai berikut :
x^{2}=\sum_{i=1}^{k}\frac{\left (O_{i}-E_{i} \right )^{2}}{E_{i}}Dimana
Oi = jumlah observasi kasus pada kategori ke i
Ei = jumlah harapan kasus pada kategori ke I jika H0 benar
K = jumlah kategori
Pada uji McNemar kita hanya tertarik mengamati cell-cell yang mengalami perubahan. Oleh karena itu, jika A adalah jumlah observasi kasus dengan perubahan jawaban dari + ke – dan D jumlah observasi kasus denan perubahan jawaban dari – ke +, dan (A + D)/2 adalah jumlah harapan kasus pada cell A dan D, maka:
x^{2}=\sum_{i=1}^{k}\frac{\left (O_{i}-E_{i} \right )^{2}}{E_{i}}x^{2}=\frac{\left [A-(A+D)/2 \right ) ]^{2}}{(A+D)/2}+\frac{\left [D-(A+D)/2 \right ) ]^{2}}{(A+D)/2}
x^{2}=\frac{\left (A-D \right )^{2}}{A+D} dengan df=1
Sampling distribusi x^{2} dapat dihitung dari rumus diatas dan jika H0 benar, maka distribusinya adalah distribusi Chi-square dengan df = 1.
Coorection for continuity. Samping distribution x^{2} akan menjadi lebih tepat jika dilakukan koreksi untuk kontinyuitas. Koreksi ini diperlukan karena distribusi kontinyu (Chi-square) digunakan untuk mendekati distribusi diskrit (x^{2}). Apabila semua harapan frekuensi nilainya kecil, maka hasil uji akan lemah. Adapun rumus korelasi kontinyuitas adalah :
x^{2}=\frac{\left (|A-D|-1 \right )^{2}}{A+D} dengan df=1Nilai signifikansi x^{2} hitung dapat ditentukan berdasarkan tabel yang memberikan nilai kritis distribusi Chi-Square untuk df dari 1 sampai 30. Jika nilai hitung x^{2} lebih besar atau sama dengan nilai tabel Chi-square dengan df=1, maka hipotesis nol ditolak.
Untuk memberikan gambaran penggunaan uji McNemar, kasus di bawah ini akan kita analisis.
Kasus
Selama masa kampanye presiden Amerika, telah dilangsungkan debat televisi antara kedua kandidat presiden yaitu Ronald Reagen dan Jimmy Carter. Seorang peneliti ingin mengetahui apakah debat kandidat presiden ditelevisi untuk pemilihan presiden Amerika 1980 merupakan sarana efektif untuk merubah preferensi pemilihan kandidat bagi para penonton televisi. Kita mengharapkan, jika kandidat (Reagen dan Carter) sama efektifnya, maka akan ada perubahan yang sebanding dalam preferensi penonton untuk memilih kandidat. Namun demikian, jika salah satu kandidat lebih efektif atau persuasif didalam kampanye, maka akan ada perubahan signifika preferensi dari suatu kandidat ke kandidat yang lain. Untuk menguji efektivitas debat televisi, peneliti memilih sampel 70 orang secara random sebelum debat dimulai dan menanyakan preferensi mereka terhadap kedua kandidat presiden. Setelah debat televisi selesai, responden 70 orang ditanya lagi tentang preferensi mereka terhadap kandidat. Hasil tabulasi jawaban responden dapat dilihat pada tabel di bawah ini.
| Preferensi sesudah debat TV | ||
| Preferensi seblum debat TV | Reagan | Carter |
| Carter | 13 | 28 |
| Reagen | 27 | 7 |
Langkah Analisis
- Hipotesis nol. H0 : Dianatara penonton TTV yang berubah preferensinya, probabilitas penonton akan berubah preferensi pilihan dari Reagen ke Carter adalah sama dengan probabilitas penonton yang akan berubah pilihan dari Carter ke Reagen.
Hipotesis Alternatif. H1 : Ada perbedaan perubahan preferensi.
atau
H0: P [Reagen -> Carter] = P [Carter -> Reagen]
H0: P [Reagen -> Carter] ! P [Carter -> Reagen] - Statistik Uji McNemar untuk signifikansi perubahan dipilih karena peneliti menggunakan dua sampel berhubungan (berpasangan) yaitu subyek yang sama diukur dua kali, uji ini merupakan uji "sebelum dan sesudah" dan menggunakan skala nominal (kategori).
- Tingkat signifikansi alpha = 0.05 dan N jumlah penonton sebelum dan sesudah menonton debat kandidat presiden = 70.
- Samping distribution. Tabel Chi-square memberikan nilai kritis distribusi Chi-square untuk berbagai tingkat signifikansi. Sampling distrubusi x^{2} yang dihitung akan memiliki distribusi asymptotically sebagai Chi-square dengan df=1.
- Daerah penolakan. Oleh karena H1 tidak memberikan arah perbedaan, maka daerah penolakan adalah non-direcional. Daerah penolakan adalah semua nilai x^{2} yang begitu besar dan probabilitas yang berhubungan terjadinya dibawah H0 0.05 atau lebih kecil dari 0.05.
- Keputusan. Dari data pada tabel Preferensi Responden terhadap Kandidat Presiden Sebelum dan Sesudah Debat TV, diketahui bahwa A = 13 yaitu jumlah penonton yang berubah preferensi dari Carter ke Reagen, dan D = 7 jumlah penonton yang berubah preferensi dari Reagen ke Carter. B = 28 dan C = 27 adalah jumlah penonton yang tidak berubah preferensinya.
x^{2}=\frac{\left (|A-D|-1 \right )^{2}}{A+D} dengan df=1
x^{2}=\frac{\left (|13-7|-1 \right )^{2}}{13+17}
x^{2}=\frac{\left (5 \right )^{2}}{20}=1.25
Tabel Chi-square menunjukkan bahwa H0 benar dan df=1 memiliki probabilitas bahwa x^{2}\geq 3.84 atau p=0.05 . Oleh karena Chi-square hitung 1.25 < nilai tabel Chi-square 3.84, maka kita tidak dapat menolak H0 yang menyatakan bahwa kedua kandidat sama efektifnya didalam merubah preferensi penonton.
Analisis McNemar Test dengan program SPSS
Pertama yang perlu dilakukan adalah menyusun data observasi supaya dapat dibaca oleh SPSS sebagi berikut :
cell A adalah jumlah responden yang berubah dari + ke - (atau dari -1 ke 1) = 13cell D adalah jumlah responden yang berubah dari - ke + (atau dari 1 ke -1) = 7
cell B adalah jumlah responden yang berubah dari + ke + (atau dari 1 ke 1) = 28
cell C adalah jumlah responden yang berubah dari - ke - (atau dari -1 ke -1) = 27
- Buat file seperti keterangan di atas lalu simpan di excell atau di spss.
- Dari menu SPSS pilih menu Analyze kemudian pilih Non Parametric Tests lalu pilih Legacy Dialogs dan pilih Two-Related-Sample Test
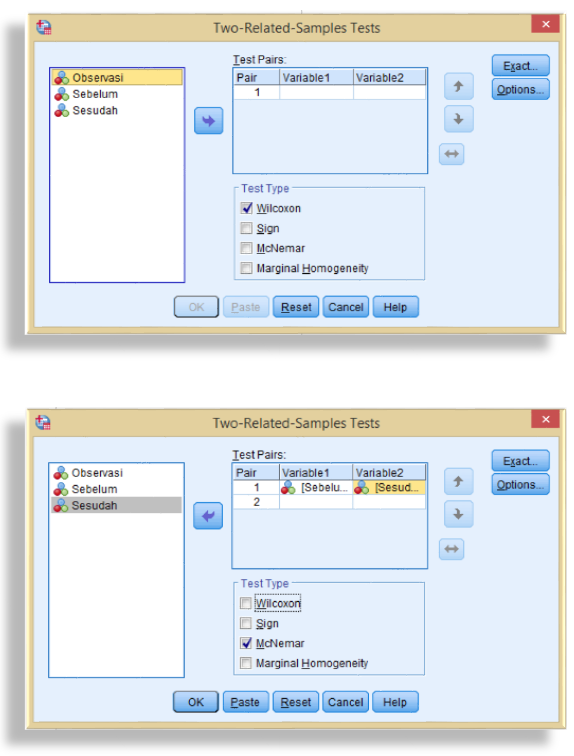
- Tampak dilayar tampilan windows Two-Related-Sample Tests
- Isikan pada Test Pairs dengan variable Sebelum pada kolom variable1, dan variabel Sesudah pada kolom variable2. Kemudian centang McNemar dan hilangkan centang Wilcoxon (default SPSS).
- Terakhir tekan OK
Interpretasi Output SPSS
Hasil tampilan SPSS menunjukkan hal sama yaitu responden yang tidak berubah preferensinya dari Pilihan Carter ke Carter ada 28 orang, responden yang tidak berubah preferensi dari pilihan Reagen tetap ke Reagen 27 orang, responden yang mengalami perubahan preferensi setelah debat TV dari Carter ke Reagen 13 orang dan yang berubah preferensi pilihan dari Reagen ke Carter 7 orang. Hasil uji statistik menunjukkan nilai probabilitas sebesar 0.263. Nilai probabilitas ini jauh diatas alpha = 0.05, maka dapat disimpulkan kita tidak dapat menolak hipotesis nol atau berarti kedua kandidat memliki efektivitas yang sama dalam mempengaruh penonton.