Sign test sesuai dengan namanya mendasarkan pada arah perbedaan antara dua pengukuran dan bukan mendasarkan pada pengukuran kuantitatif dari data. Uji Sign khususnya berguna untuk penelitian yang tidak memungkinkan menggunakan ukuran kuantitatif, tetapi masih memungkinkan menentukan setiap pasang observasi, manakah yang “lebih besar”. Uji Sign dapat digunakan untuk kasus dua sampel berhubungan, ketika peneliti ingin menetapkan bahwa dua kondisi yang ada adalah berbeda. Asumsi yang digunakan adalah variabel yang sedang diuji memiliki distribusi kontinyu. Uji ini tidak mengasumsikan bentuk dari distribusi perbedaan dan semua subyek tidak harus diambil dari populasi yang sama. Pasangan yang berbeda itu bisa berasal dari populasi yang berbeda dilihat dari umur, kelamin, intelegensia dst. Syarat yang diperlukan babwa setiap pasang eksperimen telah memenuhi “matching” dilihat dari variabel luar (extraneous) yang relevan.
Metode
Hipotesis nol yang akan diuji dengan Sign Test adalah:
P[X_{i}> Y_{i}]=P[X_{i}< Y_{i}]=1/2Dimana Xi adalah judgement atau skor pada satu kondisi ( sebelum treatment), dan Yi adalah judgement atau skor pada kondisi lainnya (setelah treatment). Hipotesis nol dapat juga dinyatakan bahwa perbedaan nilai median antara X dan Y adalah nol. Dalam menggunakan uji Sign, kita memfokuskan arah (direction) dari perbedaan antara setiap Xi dan Y1, dengan memperhatikan apakah tanda perbedaan positif atau negatif (+ atau - ).]ika HO benar, maka kita berharap jumlah pasangan yang mempunyai nilai Xi > Y1 sama dengan jumlah pasangan yang mempunyai nilai Xi < Y1. Iadi, jika hipotesis nol benar, kita berharap bahwa separo perbedaan adalah negatif dan separonya lagi adalah positif. HO akan ditolak jika terjadi terlalu sedikit selisih dengan satu tanda tertentu.
Sampel Kecil
Probabilitas yang berkaitan dengan terjadinya jumlah tanda “+” dan “-“ dapat ditentukan dengan distribusi binomial p = q = 1/2, dimana N adalah jumlah pasangan. Jika pasangan tidak memiliki perbedaan (perbedaannya adalah nol dan tidak mempunyai tanda), maka pasangan ini didrop dari analisis dan nilai N berkurang sebesar yang didrop. Appendix Tabel D memberikan nilai probabilitas terjadinya perbedaan dibawah HO dengan nilai sekecil x untuk N kurang atau sama dengan 35. Untuk menggunakan tabel D, nilai x kita anggap sebagai jumlah tanda yang terkecil.
Sebagai rnisal, 20 pasang sampel kita observasi. Enambelas (16) menunjukkan perbedaan pada satu arah (+) dan empat lainnya menunjnkkan perbedaan pada arah lainnya ( - ). Dalam kasus ini N = 20 dan x =4. Melihat tabel D didapat probabilitas nilai 4 (minus) atau lebih kecil dari 4 di bawah H0 ( den p=1/2) adalah 0.06 (uji satu sisi atau one—tail). Uji Sign bisa satu sisi (one-tail) atau dua sisi (two-tail). Pada uji satu sisi, hipotesis alternatifnya adalah tanda (+) atau (-) akan terjadi lebih sering (more frequently). Pada uji dua sisi, prediksinya adalah frekuensi terjadinya kedua tanda akan berbeda secara signifikan. Untuk uji dua sisi, nilai probabilitas pada tabel D dikalikan dua. Untuk memberikan contoh penggunaan uji Sign akan kita gunakan kasus berikut:
Contoh
Seorang peneliti ingin mempelajari proses pengambilan keputusan yang dilakukan oleh pasangan suami-isteri. Sampel pasangan suami-isteri secara intensif diteliti untuk menentukan persepsi peranan setiap pasangan dalam keputusan membeli sebuah rumah. Setiap pasangan mengisi kuesioner yang berisi persepsi pengaruh setiap pasangan (apakah suami atau isteri) dalam melakukan keputusan membeli rumah. Jawaban kuesioner berdasarkan skala dari dominasi suami sampai ke dominasi isteri dalam menentukan keputusan membeli rumah. Untuk setiap pasangan suami-isteri, perbedaan antara rating mereka ditentukan denggn memberi kode + (atau 1) jika suami menyatakan bahwa suami harus memiliki pengaruh yang lebih tinggi dalam keputusan membeli rumah dibandingkan keputusan suami yang lebih tinggi menurut pendapat isteri. Perbedaan akan diberi kode - (atau 0) kalau terjadi sebaliknya. Perbedaan akan diberi kode O (atau tanpa kode) jika pasangan suami-isteri tidak memiliki kesesuaian terhadap tingkat pengaruh dalam mengambil keputusan.
Langkah Analisis
- Hipotesis Nol. H0 2 suami dan isteri setuju dengan tingkat pengaruh masing-masing terhadap satu aspek dalam keputusan membeli rumah. H1: suami menyatakan bahwa mereka harus mempunyai pengaruh lebih dalam memntuskan membeli rumah dibandingkan dengan isterinya.
- Uji statistik. Skala pengukuran yang digunakan dalam studi ini adalah skala order (urutan). Informasi dalam pengukuran akan tetap dapat dipertahankan jika perbedaan dua rating dari setiap pasangan suami-isteri dinyatakan dalam tanda + atau — ( 1 atau O). Setiap pasangan suami-isteri dalam studi ini adalah “Matched pair”. Uji Sign sesuai dengan data seperti dinyatakan di atas.
- Tingkat signifikansi. on = 0.05 dan N adalah jumlah pasangan suami-isteri pada satu kondisi = 17.
Sampling distribution. Probabilitas terj adinya nilai sebesar x dapat diperoleh dcngan distribusi binomial untuk p = q = 1/2. Nilai probabilitas dapat dilihat pada Tabel D. - Daerah penolakan. Oleh karena H1 memprediksi arah perbedaan, maka daerah penolakan adalah satu sisi (one-tail). Daerah penolakan berisi semua nilai x (dimana x adalah jumlah +, oleh karena prediksi H1 perbedaan positif akan dominan) untuk probabilitas satu sisi terjadinya jika HO benar adalah sama atau kurang dari 0.05.
- Keputusan. Judgement pengaruh setiap pasangan suami-isteri diukur dengan tujuh skala penilaian. Pada skala ini rating 1 menunjukkan bahwa isteri harus mempunyai otoritas penuh untuk mengambil keputusan, sedangkan rating 7 menunjukkan judgement bahwa suami harus mernpunyai otoritas penuh untuk mengambil keputusan, dan nilai tengah menunjukkan tingkat pengaruh tengah. Tabél 3.4 dibawah ini memberikan rating pengaruh untuk setiap suami (S) dan isteri (I) diantara 17 pasangan suami-isteri.
Tabel 3.4 menunjukkan bahwa ada tiga pasangan suami-isteri yang mcmpunyai perbedaan yang berlawanan dengan prediksinya dan diberi kode - (atau 0), dan tiga pasangan lainnya tidak mempunyai kesesuaian dalam mengambil keputusan dan diberi kode O, sedang jumlah sampel dikurangi dengan tiga pasangan ini menjadi N = 17 - 3 = 14. Sisa pasangan suami-isteri menunjukkan perbedaan yang sesuai dengan prediksi. Untuk data tabel 3.4, x adalah jumlah tanda positif = ll, dan N adalah jumlah pasangan (matched pairs) = 14.
Appendix Tabel D menunjukkan untuk N = 14, probabilitas observasi x2 lebihbesar samadengan 11 dengan uji satu sisi sebesar 0.0Z9. Oleh karena probabilitas ini dibawah alpha = 0.05,maka kita menolak HO dan menerima H1 yang menyatakan bahwa suami percaya bahwa mereka harus memiliki pengaruh yang lebih besar dalam keputusan membeli rumah daripada isterinya.
Tabel Pengaruh Dalam Pengambxlan Keputusan Pasangan Rating Pengaruh Arah perbedaan Tanda Suami Isteri
Data ini akan kita uji dengan program SPSS dengan langkah sebagai berikut. Simpan format data seperti tabel untuk tiga kolom pertama yaitu variabel Pasangan, Suami dan Isteri dan simpan dalam program excel dan diberi nama file Sign2.xls.
Langkah Analisis dengan SPSS
- Buat file untuk Sign Test dengan variabel dan datanya seperti tabel di atas.
- Dari menu SPSS pilih menu Analyze kemudian pilih Non Parametric Tests lalu pilih Legacy Dialogs dan pilih Two-Related-Sample Test
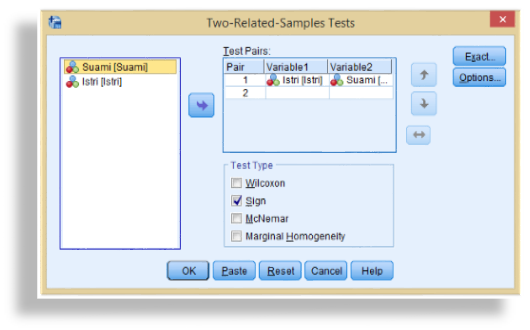
- Tampak dilayar tampilan window Two-Related-Samples Test
- Isikan variabel yang akan dianalisis pada Current Selection variable1 adalah Istri dan Variable2 adalah Suami. Isikan pasangan Suami-Isteri pada kotak Test Pair(s) List
- Pilih Test Type Sign
- Abaikan yang lain dan tekan OK
Interpretasi Output SPSS
Tampilan output SPSS menunjukkan bahwa jumlah perbedaan negatif ada 3 dan jumlah perbedaan positif ada 11, dan ada 3 yang tidak memberikan perbedaan (disebut ties). Nilai probabilitas uji Sign adalah 0.057 untuk uji dua sisi. Oleh karena uji kita adalah satu arah (satu sisi) maka nilai probabilitas dibagi dua menjadi 0.029. Nilai probabilitas ini sama dengan perhitungan dengan tabel D. Karena probabilitas 0.029 lebih kecil dari Ot = 0.05, maka dapat disimpulkan bahwa kita menolak H0 dan menerima H1 yang menyatakan bahwa suami percaya bahwa mereka harus memiliki pengaruh yang lebih besar dalam keputusan membeli rumah daripada isterinya.