Pada postingan yang lalu telah dibahas model regresi semi-log dalam kaitannya dengan model regresi dengan beberapa pelanggaran terhadap asumsi klasik yaitu terjadinya heteroskedastisitas dan tidak terpenuhinya normalitas pada distribusi data sampel. Telah dicoba model regresi semi-log dan ternyata masih terdapat heteroskedastisitas pada variabel salbegin (Beginning Salary). Untuk itu perlu dilakukan analisis dengan model lainnya yaitu model regresi double-log.
Langkah berikutnya kita coba dengan merubah model regresi menjadi model regresi double-log, yaitu baik variabel dependen maupun variabel independen semuanya dirubah dalam bentuk logaritma natural seperti di bawah ini.
LnSalary = \beta 1 + \beta 2 LnSalbegin + \beta 3 LnEduc + \beta 4 LnPrevexp + \muLangkah analisis
- Dari menu utama SPSS, pilih Analyze kemudian submenu Regression, lalu pilih Linear.
- Tampak di layar Windows Linear Regression.
- Pada kotak Dependent isikan variabel LnSalary.
- Pada kotak Independent isikan variabel LnSalbegin, LnEduc, dan LnPrevexp.
- Pada kotak Method pilih Enter.
- Untuk mendapatkan nilai residual dari persamaan regresi ini, pilih Save dan pilih Unstandardized Residual.
- Untuk menguji asumsi klasik Multikolinearitas, pilih statistics dan aktifkan Covariance Matrix dan Collinearity Diagnostics.
- Untuk menguji asumsi klasik Autokorelasi aktifkan kotak Durbin-Watson.
- Tekan continues.
- Untuk menguji asumsi klasik Homoskedastisitas, pilih Plots dan isikan pada kotak Y = SRESID dan pada kotak X = ZPRED.
- Untuk menguji asuksi klasik normalitas residual aktifkan Histogram dan Normal Probability Plots.
- Tekon continue dan abaikan yang lain lalu OK
Catatan: lihat uji Lilieford
Disini walaupun menggunakan Tes One Sample Kolmogorov-Smirnov namun hasil uji statistik yang ditampilkan atau digunakan adalah nilai Liliefors. Terlihat bahwa nilai Test Statistic Lilieford sebesar 0.058 dengan tingkat signifikansi 0.001 yang berarti nilai residual terdistribusi secara normal. Karena nilai Test Statistic (0.058) dengan tingkat signifikan 0.001 lebih kecil daripada nilai Lilieford tabel (0.886 / sqrt(450) = 0.042) dengan tingkat signifikansi 0.05.
Dengan scatter plots tampak bahwa hasil observasi menyebar secara acak di sekitar titik 0 pada sumbu Y dan hal ini dapat disimpulkan bahwa model regresi homoskedastisitas. Untuk meyakinkan kita perlu lakukan uji Glejser sebagai berikut.
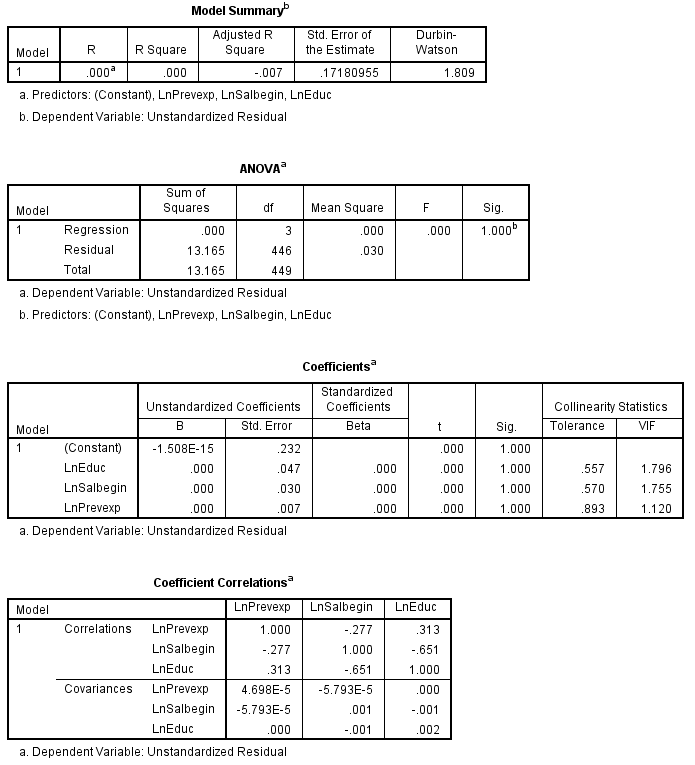
Hasil regresi terlihat tidak ada satupun variabel independen yang signifikan. Hal ini berarti tidak ada heteroskedastisitas atau model regresi homoskedastisitas.
Jadi dapat disimpulkan model yang memenuhi asumsi klasik multikolinearitas, autokorelasi, normalitas residual dan homoskedastisitas adalah model double-log seperti di bawah ini.
LnSalary = \beta 1 + \beta 2 LnSalbegin + \beta 3 LnEduc+ \beta 4 LnPrevexp + \mu .